本研究では，多数の分散した動的要素の挙動が協調し，全体としてまとまった全体挙動を示すための原理に関する基礎的な理論研究，およびその原理を用いた超並列画像処理システムや群ロボットシステムにおける協調動作の獲得といった応用研究を行っている．

　多数の動的要素を持つ大規模なシステムは，状態空間が高次元となる．しかし一般に，状態となる物理量の種類は，「位置と運動量」や「電圧と電流」といった具合に少ない場合が多い．つまり大規模システムにおいては，一般に同じ物理量が異なった“場所”に存在するため，状態空間が位相構造（この状態量は，あの状態量よりもその状態量に近い，などといった，空間的な距離構造）を持つ．この位相構造を表現する方法として，

1. 連続的な空間位相を表す変数を導入する方法
2. グラフ（ネットワーク）により空間位相を表す方法

　システム全体が協調した状態を，１次元の秩序パターン（(1)の場合は空間変数のスカラ関数，(2)の場合はグラフ上のスカラ関数）で表現する．この時，システム全体の挙動を調べるには，それらのスカラ関数が時間とともにどのように変化するかを解析すればよい．ここでは，システム全体を評価するポテンシャル汎関数が存在し，そのポテンシャル汎関数の勾配に従ってその値を減少させるように変化する関数空間における勾配系を用いて解析を行う．ポテンシャル汎関数がスカラ関数の空間微分の１次の項までで表される時，(1), (2)の場合の両方とも（非線形）反応拡散方程式が得られた[文献1)参照]．これは，

1. それぞれの動的要素は自分と相互作用している周囲の状況から自己の動作を決定していること，
2. それにも関わらず，システム全体はポテンシャル汎関数を減少させるようにまとまった挙動を示すこと，

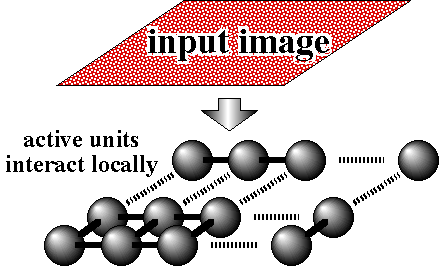
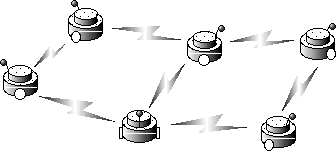
　動的要素を画素と見なしてこの結果を応用すれば，動的な画素による超並列画像処理システムができる（ Fig. 1参照）．また，動的要素を移動ロボットと見なした場合は，群ロボットシステムが協調動作を実現する原理となる（Fig. 2参照）．

   Keywords: Evolution Equation, Gradient System, Potential Functional, Graph

参考文献

1. 湯浅秀男，伊藤正美：グラフ上の反応拡散方程式と協調のアルゴリズム，第８回インテリジェント・システム・シンポジウム講演論文集, pp.1-6, 九州, October 1998.