A theory of coordination for micro dynamics and self-organization

There are many kinds of self-organizing systems in the world, almost all of which have some common properties. Here, it is focused on the property that almost all of them consist of many subsystems which are interacted only with their neighbors. They also have the same physical quantities, which are continuous against space and time. For example, the flow of fluid in Benard convection, the concentration of reactants in Belousov-Zhabotinsky reaction, and so on. In these situations, each subsystem is able to observe only its neighbors. In other words, each subsystem observes the whole system partially from inside, then such a system is one of the internal observation systems. This research considers how to treat such internal observation systems theoretically.

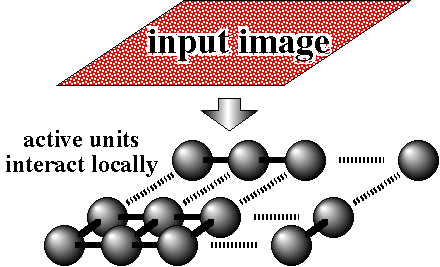
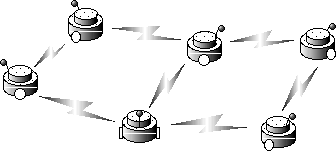
Almost all self-organizing systems, which are generally modeled by spatiotemporal evolution equations, are able to be regarded as internal observation systems. Therefore, it is started here to analyze the time evolution of spatiotemporal evolution equations in function space. First, self-organized spatial pattern is expressed by function of position which defines the value of the physical quantity at this position. Then, the spatiotemporal evolution equation determines the trajectories of pattern in function space. One of the simplest dynamics is generated by a gradient system whose velocity vector field is proportional to the gradient vector field of a potential function. Therefore, if we design a potential functional whose minimum points correspond to some desired patterns, the gradient system organizes one of the desired pattern. At this time, the micro dynamics expressed by the evolution equation is derived by differentiating the potential functional with respect to pattern. These subsystems whose behavior obeys the micro dynamics cooperate with their neighbors and generate one of the desired orders. Generally, evolution equations express the spatiotemporal behavior of continuous media. However, artificial systems do not usually consist of continuous media, but have the structure that subsystems connect with some of them, expressed by a graph. Therefore, it is important to expand evolution equation on graph. This expansion make this theory to be able to used for parallel image processing system, multi-mobile robots system, and many real systems(see figure 1 and 2).

1. Hideo YUASA and Masami ITO: Internal Observation Systems and a Theory of Reaction-Diffusion Equation on a Graph, Proc. of 1998 IEEE International Conference on Systems, Man, and Cybernetics(SMC'98), U.S.A., pp.3669-3673(1998)

Fig. 1 Autonomous-decentralized image processing Fig. 2 Coordination of multi mobile robots